Maquinas de Turing.

Otra forma de caracterizar la clase de las funciones computables se hace mediante las llamadas máquinas de Turing ³³. Estas son máquinas formales, es decir sin cables ni componentes físicos. Su finalidad es definir los cálculos a partir de las operaciones más sencillas posibles, y utilizando las cuales calcular efectivamente funciones dadas. Las funciones que así pueden realizarse se llaman funciones calculables o computables.

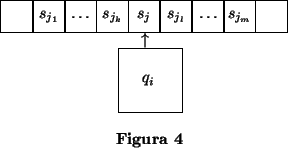
Este tipo de máquina consta hipoteticamente de una unidad de control capáz de interpretar las instrucciones que reciba, y de una cabeza lectora que permite leer el contenido de una de las casillas en que esta dividida una memoria lineal, ilimitada en ambas direcciones de sus extremos.

La máquina en su funcionamiento pasa por diferentes estados $q_i$ en instantes $t$ sucesivos. El argumento de la función que queremos calcular estará almacenado previamente en la memoria, y en el instante inicial, antes de que la máquina comience a funcionar, la cabeza lectora apuntará al símbolo más a la izquierda del argumento. A partir de ese momento la máquina realizará operaciones, que dependerán del estado en que ella se encuentre, y del símbolo que en ese momento lea la cabeza lectora. Con estas operaciones se podrán realizar las siguientes atreas: sustituir el símbolo leído por otro, pasar a leer el símbolo que esta en memoria a la derecha del símbolo leído, pasar a leer el símbolo que esta en memoria a la izquierda, o saltar directamente a ejecutar otra instrucción si se cumple una condición especificada ³⁴; en todos los casos, y una vez ejecutada la tarea indicada, se pasaría al estado que tambien se indica en la propia instrucción.

Estas instrucciones, o cuaternas, las podemos representar e interpretar así:

$q_i$ $s_j$ $s_k$ $q_l$ :	si estando en el estado $q_i$ se lee el simbolo $s_j$, entonces $s_j$ se cambia por $s_k$ y se pasa al estado $q_l$
$q_i$ $s_j$ R $q_l$ :	si desde $q_i$ se lee $s_j$, entonces se pasa a leer la casilla situada a su derecha y se cambia al estado $q_l$
$q_i$ $s_j$ L $q_l$ :	si desde $q_i$ se lee $s_j$, entonces se pasa a leer la casilla a su izquierda y se cambia al estado $q_l$
$q_i$ $s_j$ $q_k$ $q_l$ :	si desde $q_i$ se lee $s_j$, entonces se cambia al estado $q_k$ o al $q_l$ según una cierta condición

donde: $q_i$ indica un estado de la máquina tomado del conjunto de estados $Q$; $s_j$ indica uno de los símbolos que pueden aparecer en la memoria tomado del alfabeto $S$; $R$ es un símbolo que indica pasar a leer la casilla de memoria situada a la derecha; $L$ es un símbolo que indica pasar a leer la casilla de memoria situada a la izquierda.

Se define una máquina de Turing $(M)$ como un conjunto finito, no vacío, de cuaternas, de forma que no contenga dos cuaternas con los dos primeros símbolos correspondientes iguales.

Indicaremos por $Q = \{q_i\}$ al conjunto de estados de la máquina, por $S=\{s_j\}$ al alfabeto de símbolos de la memoria.

En $Q$ siempre existe un estado particular, que se suele indicar por $q_0$ y llamarse estado inicial, en el que se supone está la máquina al comenzar a operar. En el alfabeto $S$ siempre figurarán, entre otros posibles, dos símbolos: el blanco ($B$), y el uno (expresado por un palote $\vert$ ) . A las cadenas formadas por símbolos de este alfabeto se las llama expresiones de memoria. Si en una expresión de memoria incluimos un único símbolo $q_i$ (que indique un estado de $Q$) siempre que no le situemos a la derecha de cualquier otro, obtendremos una expresión que llamaremos descripción instantánea de la maquina $M$.

Los números naturales se representan en estas máquinas, de la forma más simple, es decir usando un solo símbolo ( $\vert$ ). Se emplean dos clases de representación numérica; una llamada de entrada mediante la cual con un solo palote representaremos el cero, y cualquier otro número $n$ se representará por $n+1$ palotes; y la otra, llamada de salida, consiste en contar el número de palotes que hay en la expresión de memoria (ningún palote se interpretaría, en este caso, como el 0).

La descripción instantánea de la maquina $M$ en el instante inicial podría representarse por

$$q_0\, s_{i1}\, s_{i2} \,s_{i3}\ldots s_{in}$$

En cualquier otro instante una descripción instantánea sería de la forma

$$\alpha = s_{j1}\,\ldots s_{jk}\, q_i\, s_j s_{jl}\, \ldots s_{jm}$$

Para ver como funciona una máquina de Turing, veamos como se realizan las transiciones de unas descripciones instantaneas a otras. Dada una descripción instantanea $\alpha$ , en la que aparezcan el par de símbolos $q_i$ $s_j$ , buscaríamos la cuaterna de la máquina que comience con estos dos símbolos y operaríamos en consecuencia, es decir, para cada uno de los tipos de cuaternas, construiríamos la descripción instantánea siguiente, $\beta$, como indicamos a continuación:

para      $q_i s_j s_k q_l$	sería	$\beta = s_{j_1} \ldots s_{j_k} q_i s_k s_{j_l} \ldots s_{j_m}$
para     $q_i s_j R q_l$	sería	$\beta = s_{j_1} \ldots s_{j_k} s_j q_i s_{j_l} \ldots s_{j_m}$
para     $q_i s_j L q_l$	sería	$\beta = s_{j_1} \ldots q_i s_{j_k} s_j s_{j_l} \ldots s_{j_m}$
para      $q_i s_j q_k q_l$	sería	$\beta = s_{j_1} \ldots s_{j_k} q_k s_j s_{j_l} \ldots s_{j_m}$ si el número representado por cinta en ese instante pertenece a un conjunto dado $A$ , o bien si el número representado por la cinta en ese instante no pertenece a un conjunto dado $A$

En el último caso aparece el conjunto $A$, que es un conjunto de números naturales, que no forma parte de la máquina, y al que hay que consultar antes de tomar la decisión sobre una de las alternativas propuestas (es el ``oráculo" a que nos referiamos en una nota de la pagina anterior).

Si no existiese en $M$ ninguna cuaterna que comenzase por $q_i s_j$ diríamos que la descripción instantánea $\alpha$ es terminal.

En cualquiera de los casos anteriores decimos que de la descripción instantanea $\alpha$ se pasa a la $\beta$ mediante la maquina de Turing $M$, lo que se denota $\alpha \rightarrow \beta (M)$.

Llamamos computación o cálculo de una máquina de Turing $M$, a una sucesión finita de descripciones instantáneas $\alpha_1 , \alpha_2 , \ldots \alpha_n$, de forma que para $1 \leq i < n$, sea $\alpha_i \rightarrow \alpha_{i+1} (M)$, y sea $\alpha_n$ , una descripción instantánea terminal.

Para calcular una función $f : N^n \rightarrow N$, mediante una maquina de Turing, se comenzará representando la n-upla de los argumentos mediante una expresión de memoria de la forma $\vert \vert . . \vert B\vert \vert . . \vert B\vert \vert . . \vert B . . . B\vert \vert . . \vert$, a partir de la cual se formará la descripción instantánea inicial

$$\alpha_1 = q_0 \vert \vert . . \vert B\vert \vert . . \vert B\vert \vert . . \vert B . . . B\vert \vert . . \vert ,$$

a la que se aplicaran sucesivamente las cuaternas que correspondan de la maquina de Turing hasta llegar a una descripción instantánea terminal. En esta contamos el numero de palotes que contiene, y este será el valor de la función. ³⁵

Dada una función $f : N^n \rightarrow N$, no siempre existe una Máquina de Turing, mediante la cual, a partir de cualquier argumento, podamos llegar desde el estado inicial a una descripción instantánea terminal; cuando existe una tal máquina decimos que la función es computable.