- ... matem\'aticas1
- Conferencia dada en el Atenéo de Madrid en el ciclo dedicado al Año Mundial de las Matemáticas, dirigido por el Prof. Federico Gaeta
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Camarero2
- Ha sido Director del Centro de Cálculo y Profesor de Teoría de Autómatas y Lenguajes Formales de la Universidad Complutense de Madrid, y Presidente de la Sociedad Española de Historia de la Ciencia
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... chino3
- El quipu andino es un instrumento con ciertas caracteristicas análogas al ábaco.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... equil\'atero4
- La primera proposición del Libro I de los Elementos de Euclides dice: Construir un triangulo equilátero sobre una recta finita dada.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... m\'atematicos5
- Citemos solo dos libros españoles del siglo XVII: García de Céspedes Libros de instrumentos nuevos de geometría Madrid, 1606; José Zaragoza Fábrica y uso de varios instrumentos matemáticos Madrid, 1674.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... m\'atematicas",6
- Más radical es lo que el pintoresco autor Francisco Antonio Artiga dice en el titulo de su libro publicado en 1694 Modo de Medir los Planos Orizontalemente, sin saber matemáticas, ni Arismetica y sin instrumentos matemátematicos
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reglas7
- La suma, resta, multiplicación y división, son las operaciones aritméticas básicas con las que se construirán los algoritmos numéricos, análogas a cómo son básicas las que se pueden hacer con la regla y el compás para construir los algoritmos geométricos
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...logaritmos, 8
- Nepper, Mirafici logarithmorum canonis descriptio, 1614
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... aritméticas9
- Por Pascal (1623-1662) en 1640 y por Leibniz (1646-1716) posteriormente
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cosa"10
- De esta manera se denominaba en sus orígenes al álgebra antes de que su lenguaje comenzara a formalizarse; con la palabra "cosa" se indicaba a la incógnita. Así puede verse en el título del libro de Juan Bautista Tolra, publicado en Tarragona en 1619: Tratado de Arte mayor de Aritmetica, llamada Algebra o regla de la cosa
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... radicales"11
- Así para la ecuación de segundo grado
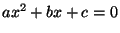 , la formula de resolución es la bien conocida:
, la formula de resolución es la bien conocida:
que corresponde al algoritmo que podría expresarse por la siguiente secuencia de las operaciones básicas :
- 1
- Calcular
- 2
- Calcular el discriminante
- 3
- Según sea el valor de
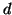 , positivo o cero (Hasta el siglo XIX, no tiene sentido hablar de la raíz cuadrada de números negativos), realizar los calculos indicados en el punto
, positivo o cero (Hasta el siglo XIX, no tiene sentido hablar de la raíz cuadrada de números negativos), realizar los calculos indicados en el punto 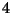 , o en el punto
, o en el punto 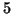 .
.
- 4
- Calcular dos raíces simples
- 5
- Calcular una raíz doble
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cuarto12
- Esta es una limitación algorítmica, análoga a la que ya se había presentado en la resolución de los problemas geometricos clásicos con la regla y el compás
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Boole13
- George Boole (1815-1864) , es un matemático inglés que recogió su teoría en un libro dedicado a las leyes del pensamiento (An investigation of the laws of thought, on which are founded the mathematical theories of logic and probabilities), publicado en Londres en 1854. También hizo aportaciones importantes a otros campos de la matemática como las dedicadas a los invariantes algebraicos, a las ecuaciones diferenciales y al cálculo de diferencias finitas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Quevedo14
- Leonardo Torres Quevedo (1852-1936) insigne ingeniero español conocido por ser uno de los grandes creadores de automatismos que aplicó a la construccion de máquinas algebraicas, del famoso jugador de ajedrez, y del telekino (primer mando a distancia). También construyó dirigibles y un transbordador sobre las cataratas del Niágara
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... identidad15
- Cuando se trata de la lógica de circuitos, para aproximarse a la aritmética binaria, se suele utilizar el símbolo
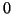 para indicar falso en lugar de la
para indicar falso en lugar de la 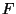 , y el
, y el 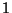 para indicar verdadero en lugar de la
para indicar verdadero en lugar de la 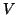 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ordenadores16
- La utilización de los relais en la construcción de circuitos es algo que desde hace tiempo ha dejado de realizarse, y estos dispositivos están ya olvidados, pero por su claridad expositiva y por su interés histórico, los hemos usado en esta descripción de los circuitos lógicos.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Babagge17
- Charles Babagge(1792-1871), diseńó una maquina The analytical engine, que solo construyó parcialmente aunque dedió a ello varios años. En esta maquina se introduce la idea de memoria para retener información. Aparte de ser el reconocido precursor de los actuales ordenadores, es tambien interesante indicar el esfuerzo que dedicó a la introducción las ideas de Leibniz en la Inglaterra de comienzos del siglo XIX, cuando todavia susistía, en el país británico, el monopolio del pensamiento de Newton en lo que se refiere al cálculo infinitesimal.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Shannon18
- Claude Shannon nació en Estados Unidos en 1916. Su tesis de master titulada A symbolic Analysis of Relay and switching circuits, se considera como fundamental para la aplicacion del algebra de Boole a la teoria de circuitos de conmutacion. Tambien es muy importante su aportacion a la teoría de la comunicación.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Neumann19
- Von Neumann (1903-1957), fue un niño prodigio; estudia matematicas en Budapest y en Berlin. Va por primera vez, como profesor visitante, a Estados Unidos en 1931, pero se traslada definitivamente en 1933 (huyendo de la situacion provocada por Alemania en Europa) al Institute for Advances Studies de Princeton, en donde coincide con Gödel y con Turing . Dedicó su actividad a múltiples areas de la matemática, pero su aportacion fue esencial para el desarrollo de la actual estructura de los ordenadors, especialemnete en la idea de programa almacenado, como ya lo describe en su First Draft of a Report on de EDVAC escrito en 1945. Tambien es uno de los creadores de la teoría de automatas y de la teoría de la programación. Es autor prolífero, entre su producción se encuentra un libro, editado en 1966 titulado Theory of Self-Reproducing Automata
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Chomsky20
- Noam Chomsky, nacido en Estados Unidos en 1928, es uno de los creadores de la lingüística matemática. Tambien es conocido por ser uno de los más eminentes pensadores disidentes americanos
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matem\'atica21
- La aparición (y su consolidación a principios del siglo XIX) de la geometría proyectiva y de las geometrías no euclideas hacen concebir nuevas geometrías que no están en armonía con nuestra intuición del espacio que obligan a una revisión del sistema lógico de Euclides (especialmente su sistema de axiomas), revisión que tiene gran trascendencia en el posterior desarrollo de la matemática y en la aparición de una nueva forma de entender la lógica que viene a confluir con el desarrollo de la lógica inglesa en la que se busca la expresión del pensamiento mediante símbolos para llegar a constituirse lo que actualmente se llama lógica matemática.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... (Morgan22
- Augustus De Morgan(1806-1871) matemático inglés que se educó en la Universidad de Cambridge pero de la que no pudo obtener los grados por negarse a firmar la declaración teológica a que estaban obligados los candidatos antes de recibirlos. Aunque publicó varios trabajos sobre los fundamentos del álgebra y sobre probabilidades, han tenido gran repercusión sus trabajos sobre lógica. En 1847 apareció su Formal Logic or the Calculus of Inference necessary and probable.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Frege23
- Friedrich Frege (1848-1925) matemático alemán que dedicó su principal actividad a intentar probar que la matemática se puede reducir a la lógica (logicismo). En 1884 publica un libro sobre los fundamentos de la Aritmética (Die Grundlagen der Aritmetik) y en 1893 otro sobre las Leyes básicas de la aritmética (Grundgesetze der Aritmetik); la paradoja de Russell mostró inconsistencia en el sistema axiomático de Frege, quien se vió obligado a modificarlo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Russell24
- Bertrand Russell (1872-1970) lógico inglés, autor, en colaboración con Whitehead, de uno de los libros más importantes de lógica mátematica titulado Principia Mathematica(1910). Es muy importante el papel que ha jugado en el desarrollo de la lógica la llamada paradoja de Russell que tiene que ver con el conjunto de todos los conjuntos que no pertenecen a ellos mismos. Su logicismo le hace llegar a considerar que el conjunto de todos los teoremas de la matemática constituyen un subconjunto de los teoremas de la lógica. Tambien es muy conocido como filósofo y por su activismo pacifista creador del llamado tribunal Russell.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Hilbert25
- David Hilbert (1862-1943) matemático alemán. Su trabajo constituye una de las mayores aportaciones al desarrollo de las matemáticas en el siglo XX. Su axiomatización de la geometría le condujeron al estudio de problemas lógicos. Publicó en colaboracion de Ackermann unos elementos de lógica teórica (Grundzüge der Theoretischen Logik) en los que busca probar la consistencia de las matemáticas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... nota26
- Una formalización de la lógica proposicional podria darse mediante el siguiente sistema:
donde el alfabeto viene dado por
El conjunto de fórmulas 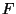 le definimos inductivamente como sigue:
le definimos inductivamente como sigue:
- 1 :
- Toda letra (llamada variable) del alfabeto :
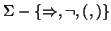 es una fórmula.
es una fórmula.
- 2 :
- Si
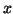 es una fórmula, entonces
es una fórmula, entonces 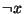 es una fórmula.
es una fórmula.
- 3 :
- Si
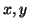 , son fórmulas, entonces
, son fórmulas, entonces
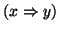 , es una formula.
, es una formula.
- 4 :
- Una palabra
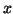 es una fórmula, si y solo si se obtiene a partir de 1,2,3.
es una fórmula, si y solo si se obtiene a partir de 1,2,3.
El conjunto 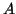 de axiomas es el siguiente:
de axiomas es el siguiente:
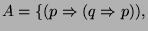
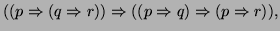
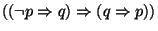
Las reglas de inferencia 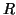 , son las siguientes, en donde
, son las siguientes, en donde 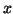 ,
, 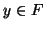 ,
,
en donde con 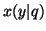 queremos indicar la fórmula que se obtiene a partir de la fórmula
queremos indicar la fórmula que se obtiene a partir de la fórmula 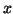 , cuando se sustituye toda aparición de la variable
, cuando se sustituye toda aparición de la variable 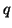 en
en 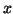 por la fórmula
por la fórmula 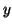 (poner
(poner 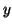 donde aparezca
donde aparezca 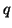 ).
).
Con este sistema, probar que la formula
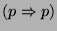 es un teorema, es construir una demostración como la siguiente:
es un teorema, es construir una demostración como la siguiente:
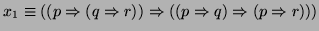 axioma
axioma
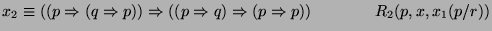
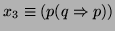 axioma
axioma



.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... \'exitos27
- Veanse las notas 4, 5 y 6.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Godel28
- Kurt Gödel (1906-1978), matemático austriaco, profesor de la Universidad de Viena; emigró a Estados Unidos en 1940; allí ejerció como profesor del Institute for Advanced Study, donde coincidió con von Neumann y con Einstein. Son muy importantes sus trabajos sobre la teoría de la demostración matemática, que dió a conocer en 1931, en los que de forma rigurosa establece las limitaciones de la teoría axiomática de conjuntos y termina con los intentos que, desde mediados del siglo anterior, se hicieron para probar la consistencia de la formalización de las matemáticas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Lulio29
- Ramon Llull (1235-1315) mallorquín, es uno de los sabios y místicos mas notables de la Edad Media, cuando comenzaba vislumbrarse el Renacimiento. Se le atribuyen el conocimiento temprano de la brújula y la invención de los protulanos. Su aportación a los inicios de una lógica simbólica es universalmente reconocida. Es autor del Ars Magna combinatoria y del Arbre de sciencia y de un trabajo sobre el arte de encontrar la verdad (Arte abreujada de trobar la veritat).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... matem\'aticos30
- Son varios los enfoques que se han dado para obordar los problemas surgidos en torno a la computabilidad, planteados tras los teoremas limitadores de Gödel. Los matemáticos que se han dedicado principalmente a este tema son, entre otros, Church, Turing, Kleene, Post, Davis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... naturales31
- Aparte del interés intrinseco de las funciones definidas entre numeros naturales, estas toman una gran importancia en la lógica a partir de la llamada numeración de Gödel que consiste en un procedimiento mediante el cual a toda expresión lingüistica se le asocia de forma única un número natural
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... sucesivos32
- Para ver como se construyen estas funciones, pongamos algunos ejemplos sencillos, que solo utilizan funciones de la base, o de las ya construidas en alguno de estos mismos ejemplos.
Suma
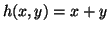 Esta función la construimos apoyándonos en las funciones
Esta función la construimos apoyándonos en las funciones 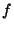 ,
, 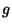 definidas de la siguiente manera
definidas de la siguiente manera
que son recursivas por emplear funciones de la base y la regla de recursion primitiva, tendríamos el siguiente esquema de recursión primitiva con el parámetro 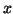
en otras palabras
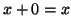 |
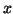 más 0 es igual a más 0 es igual a 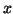 |
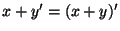 |
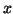 más el siguiente de más el siguiente de 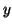 es igual al siguiente de es igual al siguiente de 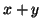 |
Producto
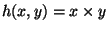 En este caso hacemos
En este caso hacemos
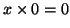 |
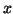 por 0 es igual a 0 por 0 es igual a 0 |
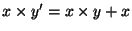 |
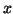 por el siguiente de por el siguiente de 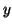 es igual a es igual a 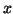 por por 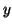 más más 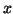 |
Factorial 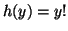 En este caso, por recursión primitiva sin parámetros, haciendo
En este caso, por recursión primitiva sin parámetros, haciendo 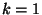 , y que la función
, y que la función 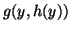 sea el producto, tenemos que
sea el producto, tenemos que
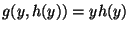 , luego
, luego
o sea:
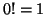 |
factorial de 0 es igual a 1 |
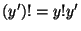 |
factorial del siguiente de 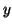 es igual a factorial de es igual a factorial de 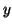 por el siguiente de por el siguiente de 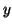 |
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Turing33
- Alan Turing (1912-1954), es un matemático inglés, que se graduó en Cambrige (UK), e hizo su doctorado (1931) en Princeton , donde coincidió con von Neumann y Gödel durante su estancia como profesor entre 1936 y 1938. Son esenciales sus trabajos sobre computación que se expresan mediante su máquina como un formalismo teórico. Tambien es conocido por sus trabajos de criptofrafía que desarrolló en el mítico laboratorio de Bletchley Park (1939-45) donde se construyó la máquina Colossus para desencriptar los mensajes cifrados por los alemanes mediante la maquina germana Enigma.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... especificada34
- Las máquinas de Turing que contienen cuaternas de este tipo se llaman no simples, o máquinas con "oráculo", elemento externo a la propia máquina que hay que consultar para tomar la decisión antes de ejecuatar este tipo de cuaternas.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... funci\'on.35
- Veamos como ejemplo, el funcionamiento de una máquina para sumar dos enteros. Dada la función
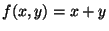 , existe una maquina de Turing que la calcula, compuesta por las siguientes cuaternas:
, existe una maquina de Turing que la calcula, compuesta por las siguientes cuaternas:
Esta maquina tiene como conjunto de estados
como estado inicial a 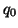 , y como alfabeto a
, y como alfabeto a
Para sumar 3 + 5 , procederíamos así:
1) La descripción instantánea inicial es
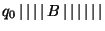 , que contiene la representacion del par de números 3 y 5 , usando la representación de entrada.
, que contiene la representacion del par de números 3 y 5 , usando la representación de entrada.
2) Los pasos sucesivos del cálculo, usando la máquina anterior son:
3) Como en la máquina dada no hay ninguna cuaterna que comience por 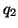 B, la máquina se detiene y por tanto la expresión
B, la máquina se detiene y por tanto la expresión
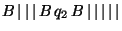 , es una descripción instantánea terminal, y el resultado, utilizando la representación de salida, es el número de
, es una descripción instantánea terminal, y el resultado, utilizando la representación de salida, es el número de  que existen en ella , es decir 8.
que existen en ella , es decir 8.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Información36
- Claude Shannon,el matemático norteamericano que uso el algebra de Boole en el diseño de circuitos fue tambien el creador de la teoría matemática de la información. Fue profesor en el MIT y colaboró con los Bell Laboratories. En 1948 publicó en el Bell Sydtem Technological Journal un artículo titulado A mathematical theory of Communication, que al año siguiente amplió en colaboración con Weaver y publicó en forma de libro con el mismo titulo.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...Cibernética 37
- El matemático norteamericano Norbert Wiener es considerado el padre de la Cibernética, teoría que difunde en un libro titulado Cybernetics, or control and communication in the animal and the machine, publicado en 1948. Fue profesor de matemáticas en el MIT (1932-1960).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...energía 38
- Es un hecho trasdendental considerar a la informacion en su naturaleza fisica, analoga a la materia y a la energia. En la comparación y relación de la información con la energía recordemos la fabula del diablillo de Maxwell que contradice al Segundo principio de la Termodinámica, y cómo la negantropía es un concepto equivalente al de información. También es un hecho evidente que la información ahorra energía.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... informacion39
- La posesión de información está dejando de ser un hecho singular, reservado a pocos, y dejando de constituir un privilegio, para pasar a ser accesible a todos y para poder circular sin la necesidad de la presencia del hombre. El efecto multiplicador de esta circunstancia es todavía inconcebible.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 5040
- En la primavera de 1956 asistí en Milán a un Convegno internazionale sui problemi dell'automatismo organizado por el CNR italiano. Fue un magno cogreso internacional (en el que participaron 15 paises entre ellos también la URSS) y cuyos trabajos se recogen en tres volúmenes; el primero dedicado a los aspectos científicos y técnicos, pero es curioso que los otros dos extensos volumenes ya se dedicaran a las implicaciones sociales de esta nueva disciplina; el volumen segundo se titula Posibilitá Tecnico-economiche, y el tercero Riflessi Economico-sociali.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
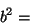
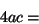
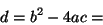
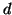 , positivo o cero (Hasta el siglo XIX, no tiene sentido hablar de la raíz cuadrada de números negativos), realizar los calculos indicados en el punto
, positivo o cero (Hasta el siglo XIX, no tiene sentido hablar de la raíz cuadrada de números negativos), realizar los calculos indicados en el punto 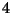 , o en el punto
, o en el punto 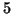 .
.
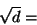
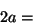
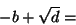
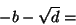
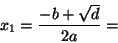
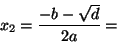
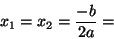
![]() le definimos inductivamente como sigue:
le definimos inductivamente como sigue:
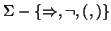 es una fórmula.
es una fórmula.
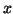 es una fórmula, entonces
es una fórmula, entonces 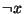 es una fórmula.
es una fórmula.
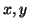 , son fórmulas, entonces
, son fórmulas, entonces
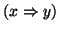 , es una formula.
, es una formula.
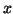 es una fórmula, si y solo si se obtiene a partir de 1,2,3.
es una fórmula, si y solo si se obtiene a partir de 1,2,3.
![]() de axiomas es el siguiente:
de axiomas es el siguiente:
![]()
![]()
![]()
![]() , son las siguientes, en donde
, son las siguientes, en donde ![]() ,
, ![]() ,
,
![]() queremos indicar la fórmula que se obtiene a partir de la fórmula
queremos indicar la fórmula que se obtiene a partir de la fórmula ![]() , cuando se sustituye toda aparición de la variable
, cuando se sustituye toda aparición de la variable ![]() en
en ![]() por la fórmula
por la fórmula ![]() (poner
(poner ![]() donde aparezca
donde aparezca ![]() ).
).
![]() es un teorema, es construir una demostración como la siguiente:
es un teorema, es construir una demostración como la siguiente:
![]() axioma
axioma
![]()
![]() axioma
axioma
![]()
![]()
![]()
![]() Esta función la construimos apoyándonos en las funciones
Esta función la construimos apoyándonos en las funciones ![]() ,
, ![]() definidas de la siguiente manera
definidas de la siguiente manera
![]() En este caso hacemos
En este caso hacemos
![]() En este caso, por recursión primitiva sin parámetros, haciendo
En este caso, por recursión primitiva sin parámetros, haciendo ![]() , y que la función
, y que la función ![]() sea el producto, tenemos que
sea el producto, tenemos que
![]() , luego
, luego
![]() , que contiene la representacion del par de números 3 y 5 , usando la representación de entrada.
, que contiene la representacion del par de números 3 y 5 , usando la representación de entrada.
![]() B, la máquina se detiene y por tanto la expresión
B, la máquina se detiene y por tanto la expresión
![]() , es una descripción instantánea terminal, y el resultado, utilizando la representación de salida, es el número de
, es una descripción instantánea terminal, y el resultado, utilizando la representación de salida, es el número de ![]() que existen en ella , es decir 8.
que existen en ella , es decir 8.